Graph Canonical / Normal Form

Most graphs may be represented as a canonical form, such as this (simplified) web-shop example:

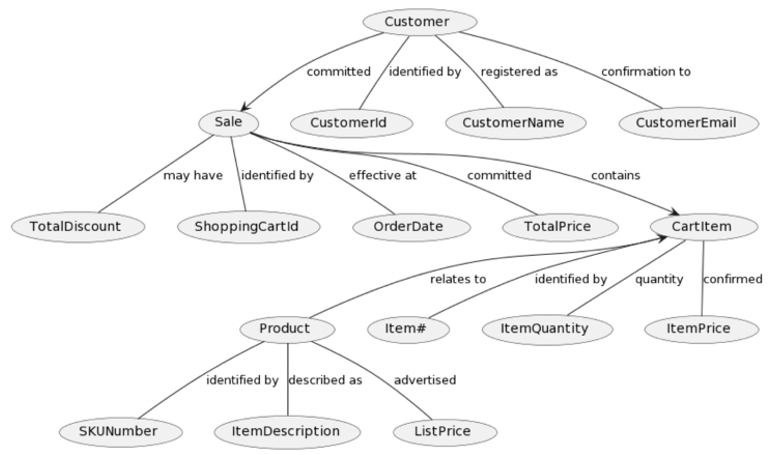
So, the components of the data model of graph normal form contains:

• A set of labels
• a set of nodes
• a set of edges
• mappings of edges to ordered pairs of nodes
• mappings of nodes and edges to the set of labels ("names").

Notice that all nodes can be named, and, equally so, all relations may be annotated with a text (i.e. a name / predicate) that enhances the readers’ understanding of the semantics of graph relations.

Graphs at this level are frequently designated as being in “graph normal form”. Most graphs may be decomposed to this level, and, when supplemented with rich annotations, such graphs are also called semantic networks.

Most databases work off “descriptors” (metadata level), which identify objects and contain their associated metadata. A (meta level) graph of all descriptors identifiers of a graph type could be a graph in normal form, which could be visualized as such having one node / vertex per descriptor.

The main extension of the canonical graph form is the addition of the concept of properties. A property graph data model representing the sample graph above could be visualized like this:

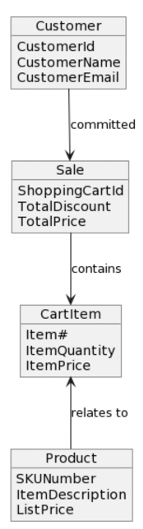
Property graphs can be seen as materializations (logical or physical) of the decomposed graph normal form representations of some semantic data models, where some properties are aggregated to become attributes of different node / vertex types, and / or also on different edge / relationship types. (Properties on relationships are not used in the sample diagram above).

The simple example above does indeed look like a relational model in third normal form. There is, however, no requirements for property graphs to be normalized in the relational (SQL) sense.

If the compositional approach is followed, many dependencies between graph elements, including properties, are derivable directly from the metadata in the graph normal form representation. If that is not available, dependencies might have to be inferred from the graph query pattern and possibly the data content at query execution time (similar to the processing in SQL).

As can be seen from the above, the property graph data model is based on the canonical data model of graph normal form extended with (sets of) property names and property values.