Graph Database Context

In mathematics, “graph theory” is the study of graphs, which are mathematical structures used to model pairwise relations between objects (text from Wikipedia on graph theory, accessed 2022-10-11). In other words, the basic building block can be pictured like this:

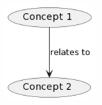
Graph thinking is not new. In fact, “The Seven Bridges of Königsberg” is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theory and prefigured the idea of topology (text from Wikipedia, accessed 2022-12-29). The theory of graphs is a rich academic discipline and is still developing.

There are many types of implementations of graphs, but almost all are based on pairwise relations between objects. Relations are semantic in the sense that they convey verbal / logical information from some business domain(s), including “is a” and “has”, but also more implicative relationships such as “identified by” or “purchased at”.

All of these kinds of relationships share the semantic pattern “subject – predicate – object”, which is the term used for the base construct in the RDF from the W3C.

Concepts are called not only that, but also object (types), entity (types) et al.

In graph theory the terms used are: Nodes / vertices / points, edges / links / lines. In graph theory the relations may be directed having starting points and end points. Hyper-relations may have multiple start / ending point types. Note that in GQL a subset of such terms is used, cf. the terms and definitions below (subclause 3.3).

Most graph paradigms share a basic, canonical, form consisting of nodes / vertices, representing concepts, as well as edges / relationships connecting the nodes / vertices to express the semantics of the concept model, including the dependencies between graph elements. More detailed information about the canonical form of graphs (also known as Graph Normal Form) is found below.

The various types of graph paradigms include more constructs, such as properties (attributes), directionality, cardinality, uniqueness, labels on graph elements and more.

The kinds of data models available to graph users are somewhat different to the strict data models found in other kinds of database paradigms. Here are some examples:

• Refined graph types are not always available, meaning that traditional schema specifications may not be necessary; unrefined graphs definitely have important use cases, and they are supported in GQL
• The level of interaction with the query system is at the level of the individual graph elements (including the properties)
• Properties may reside on both nodes / vertices and edges / relationships
• Labels may be assigned, at will, to both nodes / vertices and edges / relationships (incl. multiple labels).